Diese Seite soll kurz beschreiben, wie wir die Position des CarBot relativ zum Anfangspunkt feststellen. Noch ein Wort zum Koordinatensystem: Wir haben es so orientiert, daß der Roboter am Anfang in Richtung der positiven y-Achse ausgerichtet ist und im Koordinatenursprung steht. Die Koordinaten, mit denen wir im folgenden rechnen, sind die Koordinaten des CarBot-Mittelpunktes.
Die hierfür benötigten Sensoren sind die beiden Reflexlichtschranken, die an den Hinterrädern angebracht sind. Auf den Rädern sind jeweils 7 Reflexmarken im gleichen Abstand angebracht, d.h. pro Radumdrehung erhalten wir 7 Impulse. Da der CarBot von Gummiketten angetrieben wird, stellt der Schlupf hier kein Problem dar. (Bei anderen Konstruktionen ist es oft nicht sinnvoll, die Umdrehungen der angetriebenen Räder zu zählen, da die Antriebsräder durchdrehen könnten. Man mißt dann die Umdrehung eines nicht angetriebenen Rades.)
Bekannt ist weiterhin der Umfang U der angetriebenen Räder sowie der Abstand a der Mittelpunkte der beiden Hinterräder. Wir haben uns entschieden, den CarBot nur auf der Stelle drehen zu lassen, da sonst die Berechnung der aktuellen Position zu aufwendig geworden wäre.
Hier noch eine Auflistung aller im folgenden verwendeten Bezeichnungen mit ihrer Bedeutung:
Für die Geradeausfahrt können wir also folgendermaßen die neue Position berechnen:
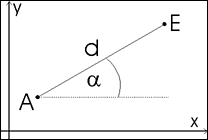
zurückgelegte Strecke d = z * (U / n)
=> Ex = Ax + d * cos(alpha), Ey = Ay + d * sin(alpha)
Um den aktuellen Drehwinkel des CarBots nach einer Drehung (auf der Stelle) zu erhalten, addieren wir zum bisherigen Richtungswinkel alpha die Winkeländerung delta alpha, die sich wie folgt berechnet:
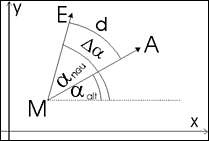
Umfang des Kreisbogens d der Drehung d = z * (U / n)
=> delta alpha = Rr * x / (2 * Pi * 0.5 * a) * 360°
=> delta alpha = Rr * x / (Pi * a) * 360°
Addition von delta alpha zur bisherigen Orientierung alpha ergibt die neue Orientierung des CarBot. Zur Erinnerung: Der Winkel des CarBot wird gegen die positive x-Achse gemessen, d.h. nach der oben vereinbarten Anfangsposition hat der CarBot am Startpunkt die Orientierung 90°!
